The shape of the earth

In order to define the earth mathematically, a geometric model of the earth’s surface must be established. The model is determined by the shape of the earth. It is a geometric model that is closer to the shape of the earth,that is an ellipsoid, which is formed by an ellipse revolving around its short axis.

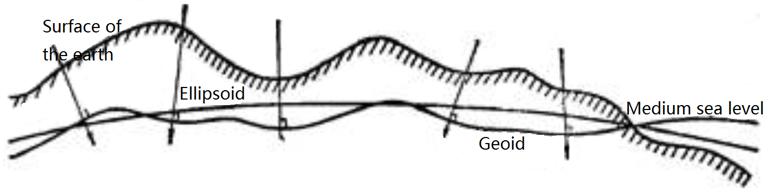
The natural surface of the earth is a rough and irregular surface, with mountains, hills and plains, as well as rivers, lakes and seas. About 71% of the earth’s surface is occupied by oceans and 29% is the continents and islands. The highest point on land is nearly 20 kilometers from the deepest point in the ocean. This uneven surface can not be expressed by mathematical formulas, nor can it be calculated. So when measuring and mapping, we must find a regular surface to replace the natural surface of the earth. When the ocean is at rest, its free surface must be orthogonal to the gravitational direction (plumb vertical direction) of the points on the surface, which we call the level surface. But there are numerousn of levels, one of which coincides with the stationary average sea level. It can be imagined that the stationary average sea surface passes through continents and islands to form a closed surface, which is the geoid (Fig. 4-1).

The shape surrounded by the geoid is called the geosphere. Because of the uneven distribution of mass inside the earth, the direction of gravity changes, resulting in an irregular geoid which is orthogonal to the direction of gravity everywhere, and still can not be expressed mathematically. Although the shape of geoid is very complex, the fluctuation is small as a whole. It is a very close ellipsoid to rotate around the axis of rotation (short axis). Therefore, in surveying and mapping, a rotating ellipsoid is used to replace the earth’s sphere, which is usually called the earth’s ellipsoid, or ellipsoid for short.

Earth’s size

Regarding the size of the earth’s ellipsoid, the element values of the ellipsoid are different due to different data. The data of ellipsoids commonly used in the world are listed as follows：

Table 4-1: Various Earth Ellipsoid Models

Ellipsoid Name	Age	Long Half Axis (m)	Short Half Axis (m)	Oblate
Bessel	1841	6377397	6356079	1：299.15
Clarke	1880	6378249	6356515	1：293.5
Clarke	1866	6378206	6356584	1：295.0
Hayford	1910	6378388	6356912	1:297
Krasovsky	1940	6378245	6356863	1：298.3
I.U.G.G	1967	6378160	6356775	1：298.25
Everest	1830	6377276	6356075	1：300.8

Radius of ellipsoid

The surface of the earth’s ellipsoid is a regular mathematical surface. The size of an ellipsoid is usually with two radii: long radius a and short radius b, or determined by a radius and flatness. The flattening *α* Represents the flatness of the ellipsoid. The calculation formula of the flatness is:α=（a-b）/a. The basic elements of these earth ellipsoidsA, B, alpha Because of the different ages, methods and regions, the results are not consistent, so there are many kinds of parameters of the ellipsoid. China adopted Hayford ellipsoid before 1952 and Krasovsky ellipsoid from 1953 to 1980. With the launch of man-made earth satellites, there are more precise conditions for estimating the earth’s shape. In 1975, the 16th International Federation of Geodesy and Geophysics adopted the first resolution of the International Association of Geodesy to announce the Earth’s ellipsoid, known as GRS (1975). Since 1980, China has adopted the new reference ellipsoid system GRS (1975). Because the difference between the long radius and the short radius of the earth’s ellipsoid is very small, when making small-scale maps, it is often treated as a sphere with a radius of 6371 km.

Elevation

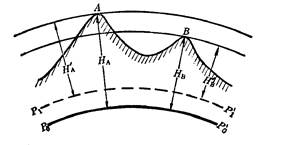
The elevation from the ground point to the geoid is called absolute elevation. As shown in Figure 2,P:sub:`0`P:sub:`0`’ For geoid, ground pointAAnd *B*To *P₀P₀’* Vertical distanceH:sub:`A`”And” *H_{B`* For *A、B* Two points of absolute elevation. The elevation from the ground point to any level is called relative elevation. As shown in Figure 2, *A、B* Two points to any level*P:sub:`1}P₁’* Vertical distanceH:sub:`A`’”And” *H_B’* For *A、B* Relative elevation of two points.

China’s Geodetic Control Network

Our country has a vast area and conducts mapping work on about 9.6 million square kilometers of land, it is necessary to divide it into several unit surveying areas, and the accuracy of surveying also meets the unified requirements. Therefore, a unified geodetic control network should be established throughout the country. The control network is divided into plane control network and elevation control network.

Geodetic coordinates: Establish a series of connected triangles on the ground and measure a precise distance as the starting edge,and use the astronomical observation method to drtermine the point(longitude, latitude and azimuth) at the two ends of the adge.The angle value of each triangle is measured by precision goniometer. According to the edge length and point position of the starting edge, the coordinates of other points can be calculated. The coordinates thus calculated are called geodetic coordinates.

In 1954, China established the origin of the geodetic coordinates in Beijing. The coordinates of the geodetic control points calculated from the origin are called the 1954 Beijing coordinate system. In 1986, China announced the establishment of a new geodetic coordinate origin in Jingyang County, Shaanxi Province, and adopted the geodetic reference ellipsoid recommended by the International Association of Geodetic in 1975. The coordinates of the geodetic control points calculated therefrom are called the geodetic coordinate system in 1980.

The starting point of China’elevation is the average sea level of the Yellow Sea. In 1956, a leveling of origin was established in Qingdao. The absolute elevation of other control points was calculated from the Qingdao leveling origin, which is called the Yellow Sea elevation system in 1956. In 1987, the State Bureau of Surveying and Mapping announced that the “1985 National Elevation Datum” to replace the “Yellow Sea Average Sea Surface” approved by the State Council in 1959. “The 1985 National Elevation Standard” is 29 mm higher than the “Yellow Sea Average Sea Level”.

Scale representation

Map scale is usually considered as the ratio of the distance on the map to the corresponding distance on the ground. Map scales can be expressed in the following ways.

1) Digital scale

This is a simple fraction or proportion that can be expressed as 1:1000000 or 1/1000000. preferably using the former. This means that the length of a map (along a particular line) is 1 mm, 1 cm or 1 inch (molecule)in length, representing 1,000,000 millimeters, centimeters or inches (denominator) on the earth’s surface.

2) Text scale

This is a description of the relationship between the distance on the map and the distance on the spot. For example, the digital scale of 1:1000000 can be described as “Fig. 1mm equals 1 km in the field”.

3) Graphical scale or linear scale

This is a straight line segment drawn on the map, often drawn in the legend box or below the map, indicating that the length of the unit on the map corresponds to the distance from the field.

Area Scale

This is related to the ratio of the area on the map to the area on the ground. It represents the ratio of a unit area (square centimeter) on the map to a specific quantity of the same square unit on the ground.

Proportionality coefficient

The relationship between the determined scale and the actual scale value is called the Scale Factor (SF). The scale coefficient can be understood in this way. First, the earth is reduced to a globe map of the selected scale, and then the spherical map is converted to a plane map. The digital scale of the above-mentioned plane map is the scale of the globe, called the main scale (or nominal scale); the real scale is the actual scale on the plane map, of course, different from place to place.

Scale coefficients can be calculated by the following formula: SF = actual scale/main scale

The formula shows that the scale coefficient is the ratio of the actual scale to the main scale of unit (1). When the scale coefficient is 2, the actual scale is twice the main scale. Scale coefficients are only evident on small-scale world maps. On large-scale maps, the scale coefficients vary only slightly with respect to 1.